【电抗器常识】脉冲电抗器之电磁场基本理论

     脉冲电抗器之电磁场的基本理论是由一组麦克斯韦方程来描述的，分析和研究脉冲电抗器之电磁场的出发点就是对麦克斯韦方程组进行研究，包括这个方程的求解与实验验证。麦克斯韦方程组由四个定律组成，分别是安培环路定律、法拉第电磁感应定律、高斯电通定律和高斯磁通定律。

      (1)安培环路定律
      无论介质和磁场强度H的分布如何，磁场中磁场强度沿任何一闭合路径的线积分等于穿过该积分路径所确定的曲面Q的电流的总和，或者说该线积分等于积分路径所包围的总电流，这就是安培环路定律，这里的总电流包括传导电流(自由电荷产生)和位移电流(电场变化产生)，如下式所示：

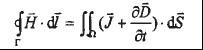
其中，r为曲面的边界，J为传导电流密度矢量，西为位移电流密度，D为电通密度。

     (2)法拉第电磁感应定律
     闭合回路中的感应电动势与穿过次回路的磁通量随时间变化率成正比。用积分表示则为：

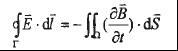
E为电场强度，B为磁感应强度。

      (3)高斯电通定律
      在电场中，不管电解质与电通密度矢量的分布如何，穿出任何一个闭合曲面的电通量等于这一闭合曲面所包围的电荷量，这里指出电通量也就是电通密度矢量对此闭合曲面的积分。其积分形式可表达如下：

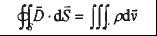
P为电荷密度，V为闭合曲面S所围成的体积区域。

      (4)高斯磁通定律
      磁场中，不管介质与磁通密度矢量的分布如何．穿出任何一个闭合曲面的磁通量恒等于零，这里指出磁通量即为磁通矢量对此闭合曲面的有向积分。高斯磁通定律的积分形式为：

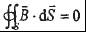
      上述四个方程构成了描述脉冲电抗器之电磁场的麦克斯韦方程组，它们对于描述脉冲电抗器之电磁场有不同的侧重点：式1表明不仅传导电流能产生磁场，变化的电场也能够产生磁场；式2是推广的电磁感应定律，表明变化的磁场同样会产生电场：式3则表明电荷以发散的方式产生电场；式4说明磁力线是无头无尾的闭合曲线。这组麦克斯韦方程表明了变化的电场和变化的磁场间相互激发、相互联系形成统一的脉冲电抗器之电磁场a其微分形式如下：
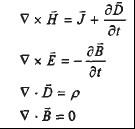